Vielen Flugschülern bereitet die Flugnavigationsaufgabe in der Flugvorbereitung große Probleme.
Ja, es ist viel Aufwand und Ja, es kann knifflig sein, wenn man es nur halbherzig erklärt bekommt es nicht regelmäßig übt damit man seine Handgriffe mit Zirkel, Lineal und der Karte auch beherrscht.
Ich möchte Euch einmal alle Schritte von einer Aufgabenstellung bis hin zur fertigen Navigationsaufgabe anhand von einer Beispielaufgabe durchrechnen und jeden einzelnen Schritt so gut wie möglich erklären.
Wir werden mit folgenden Werten arbeiten:
| Flugstrecke | EDMI (Illertissen) nach EDPJ (Laichingen) nach EDNO (Nördlingen) nach EDMI (Illertissen) |
| TAS (True Air Speed) | 160km/h |
| Wind | 280° mit 9kt |
| Spritverbrauch | 17l/h |
| Deviation | Wie im Schaubild (weiter unten) |
Was benötigen wir für die Aufgabe?
ICAO 1:500.000 Blatt Stuttgart, Navigationsbesteck bestehend aus:
Zirkel, Druckbleistift, Lineal 30cm, Geometrie-Dreieck und optional ein (DULV) Winkelmesser mit 1:500.000 zu km Skala.

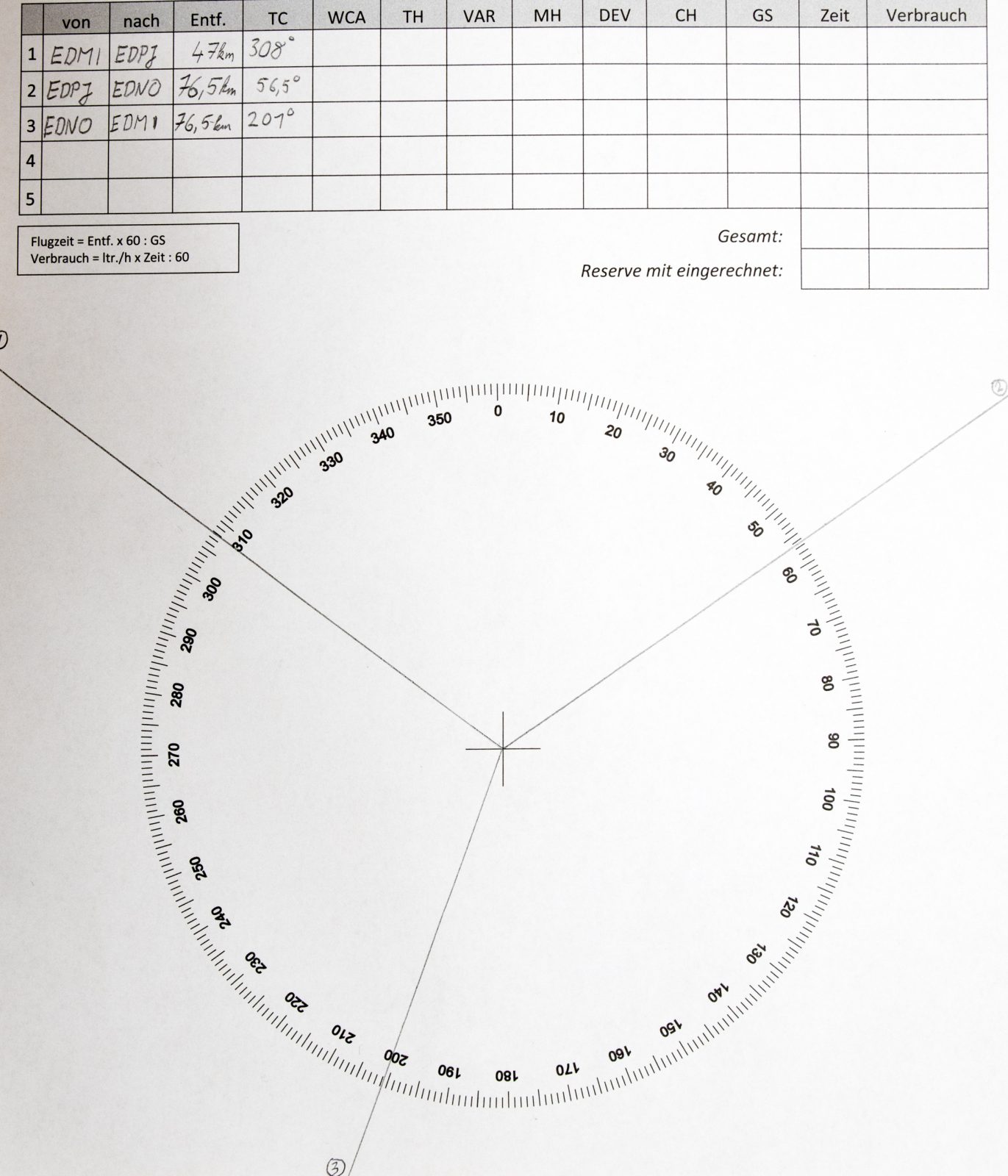
Im ersten Schritt füllen wir alle gegebenen Angaben z.B. in das DULV Formblatt oder jedes beliebige andere wie z.B. dieses hier. Der wichtige Teil ist die Kompasrose und die Streckentabelle.
Wir werden die Navigationsaufgabe im metrischen System bearbeiten. Das heißt wir werden Knoten oder Meilen in das entsprechende metrische Äquivalent umrechnen. Keine Geschwindigkeiten in km/h zeichnen und gleichzeitig den Wind in Knoten daneben setzen. Das ist ein beliebtes Problem. Also Achtung!
Die Route in die ICAO Karte einzeichnen
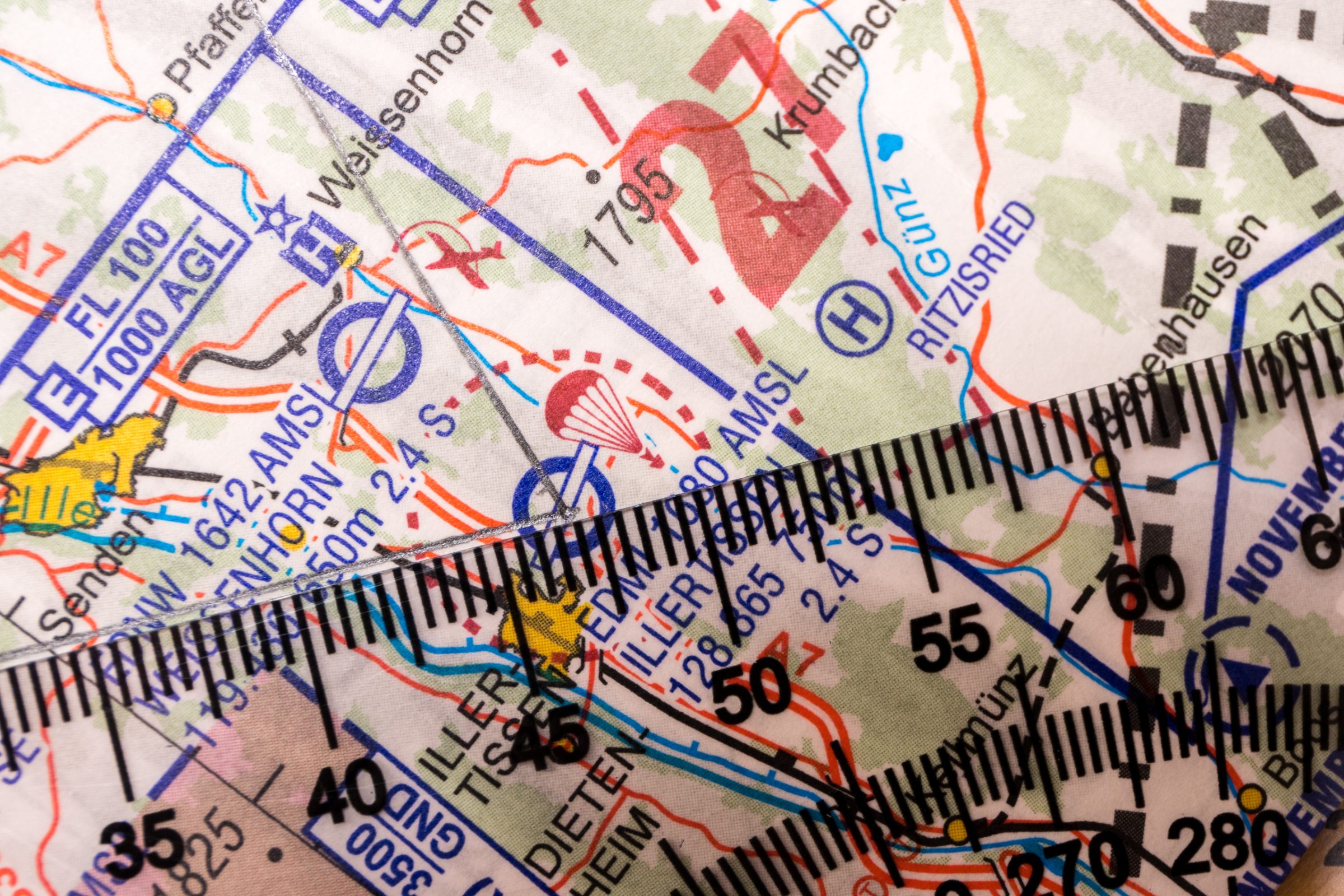
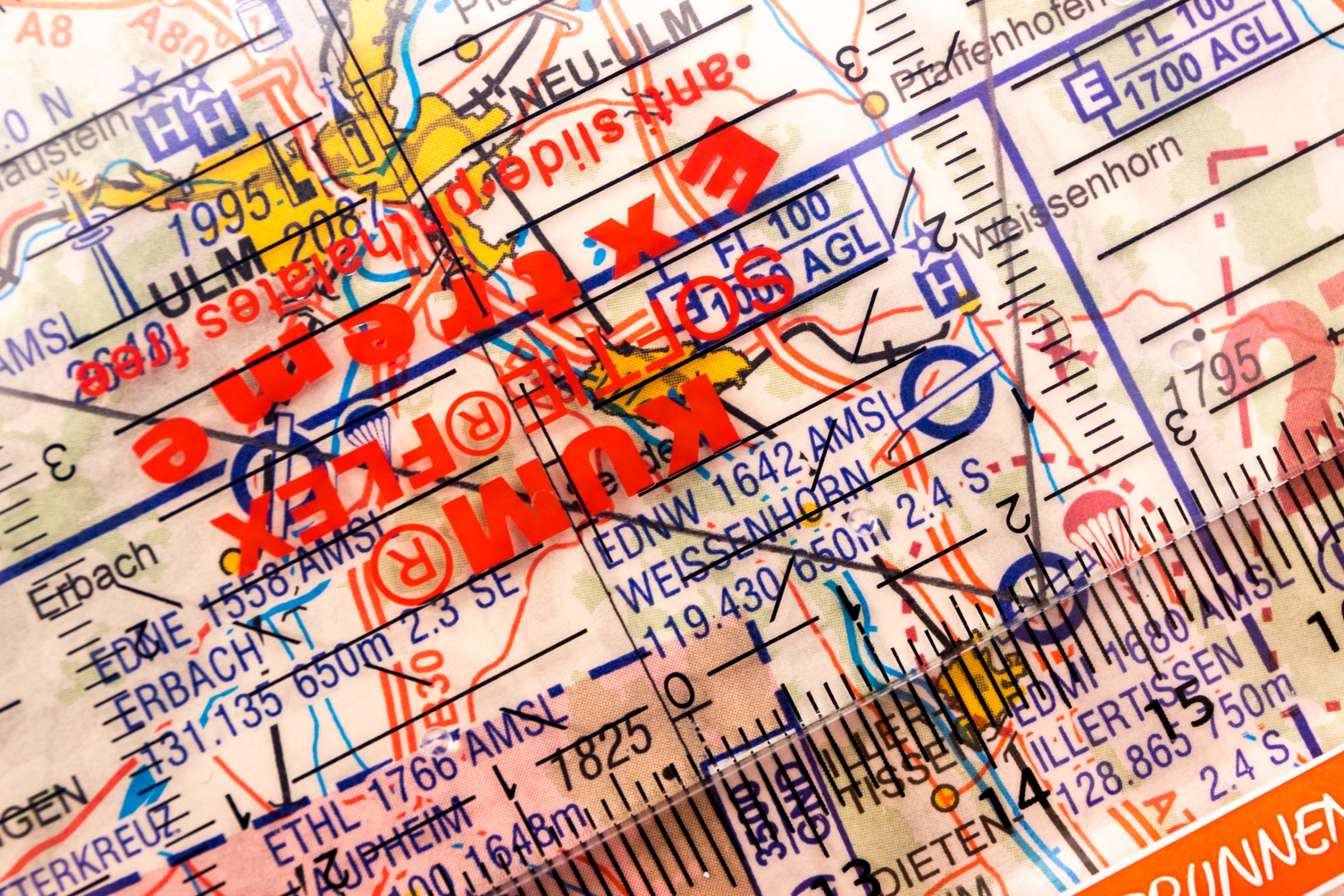
Wir suchen die Flugplätze auf der ICAO 1:500.000 Karte (Blatt Stuttgart) und verbinden die Flugplätze mit einem geraden Strich. Nutzt einen dünnen aber dennoch gut sichtbaren Bleistift wenn möglich. Ihr übermalt damit zwangsweise auch markante Landschaftsmale. Ist der Strich zu breit habt ihr im Flug ein Problem. Diese Karte nehmt ihr später mit ins Cockpit.
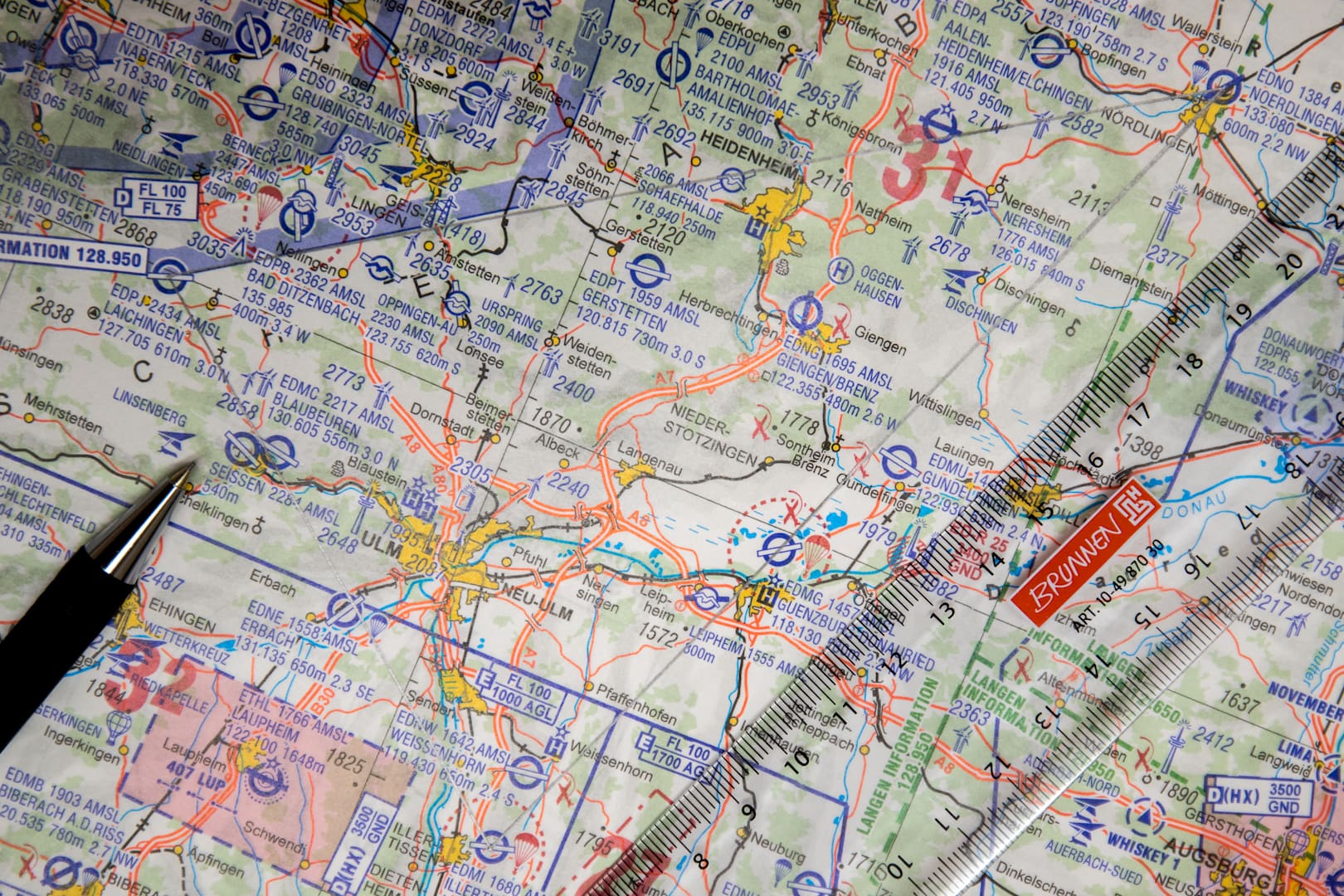
Distanzen ausmessen
Entweder Ihr habt ein Lineal, das gleich eine Kilometerskala in 1: 500 000 hat und lest die Kilometer einfach ab oder Ihr nutzt ein normales Lineal und rechnet die Distanz um.
Für die ICAO 1:500.000 Karte gillt:
1cm auf der Karte entspricht 5km in der Realität.
Oder 1mm auf der Karte entspricht 0,5km in der Realität.
Auf dem ersten Streckenabschnitt von EDMI nach EDPJ messe ich 94mm
94 * 0,5 = 47km
Wir messen alle Streckenabschnitte, rechnen die Kilometer aus und füllen unser Formblatt:
| von | nach | Entf. | |
| 1 | EDMI | EDPJ | 47 km |
| 2 | EDPJ | EDNO | 76,5 km |
| 3 | EDNO | EDMI | 76,5 km |
True Course (TC) Messen
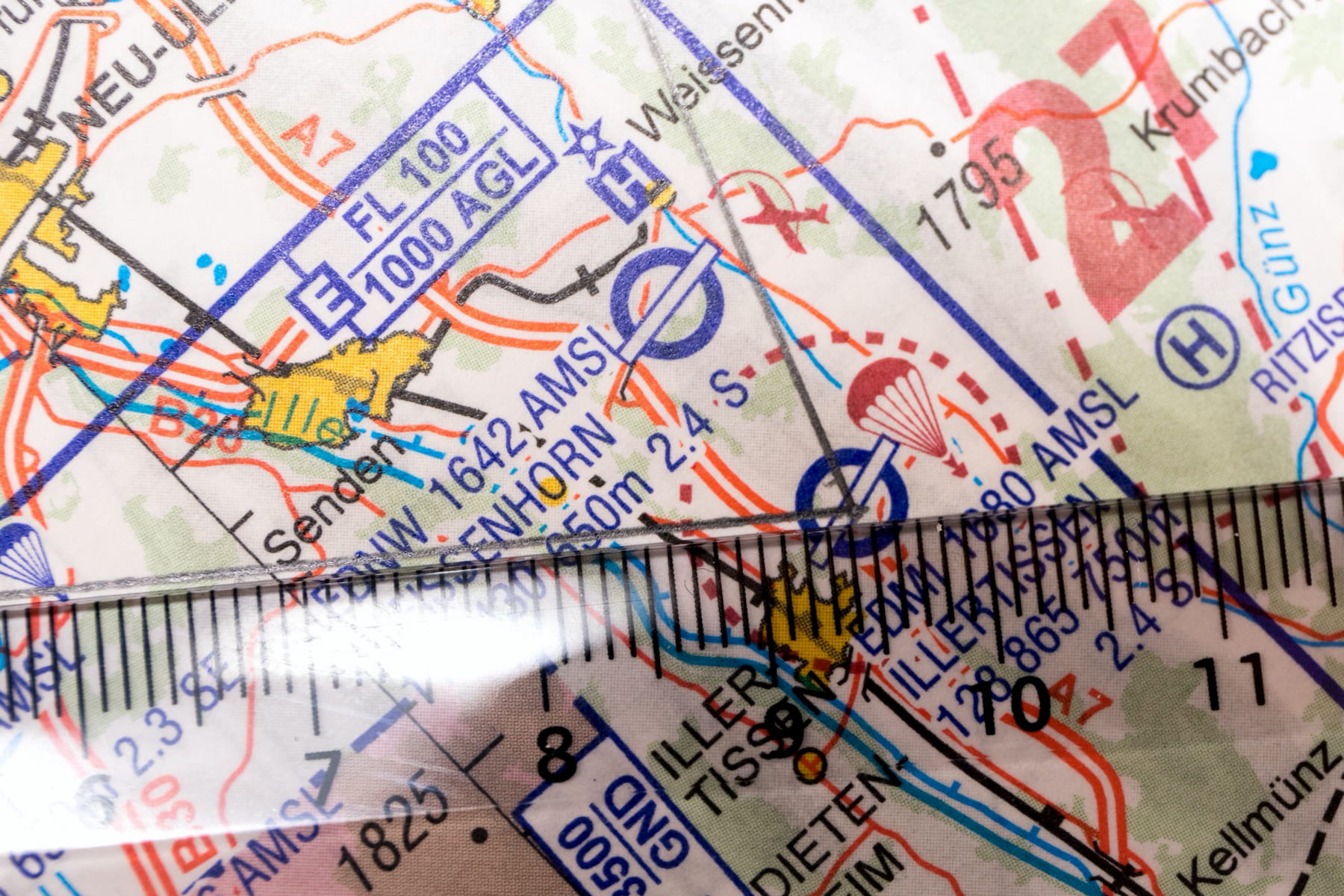
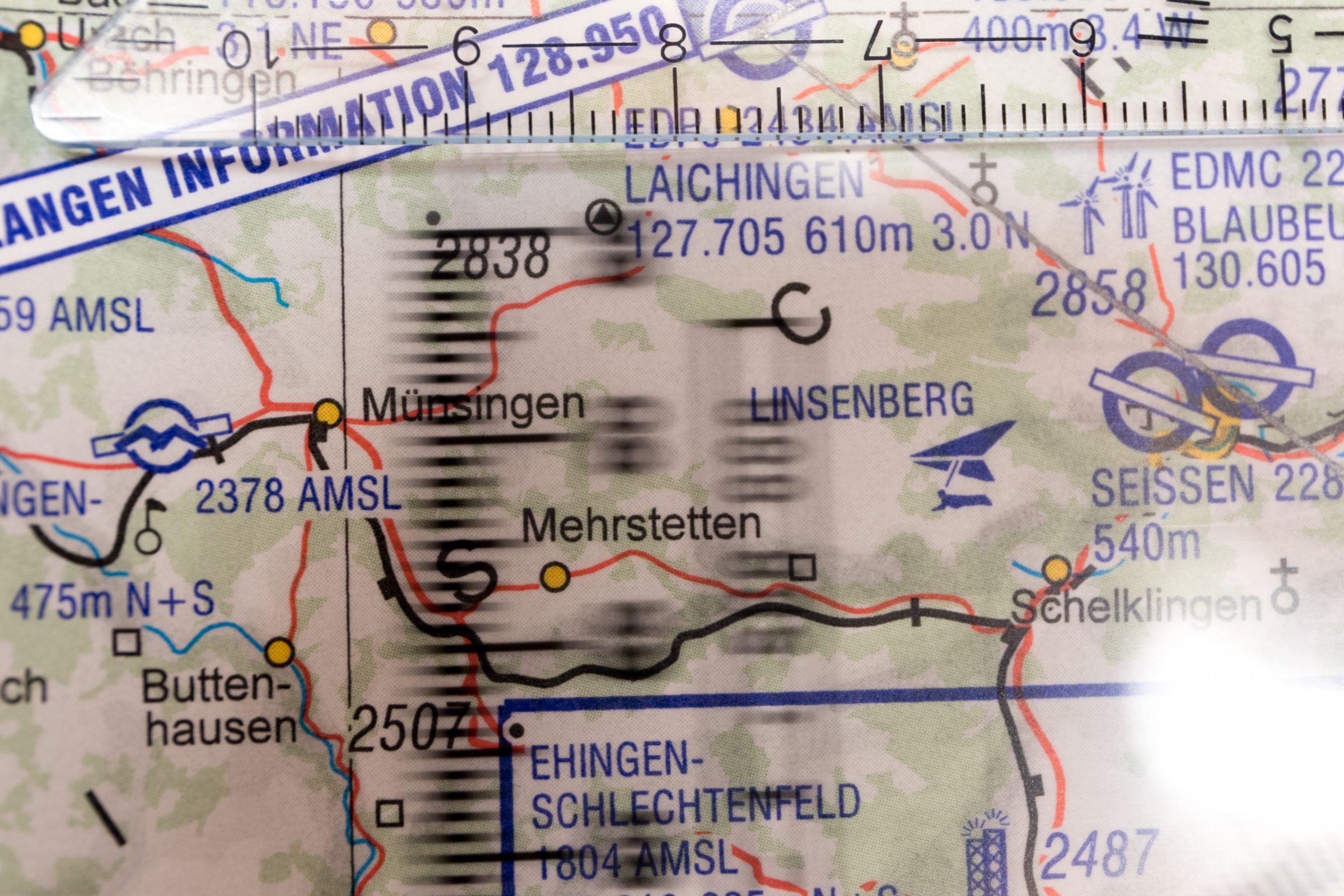
Wir benötigen den Winkel zwischen unserer gezeichneten Kurslinie und dem geographischen Nordpol. Meridianlinien sind die vertikalen schwarzen dünngezeichneten Linien auf der ICAO Karte. Diese werden in 0,5er Schritten auf den Karten dargestellt. Am oberen Rand der Karte kann man z.B. den 10. Längengrad ablesen.
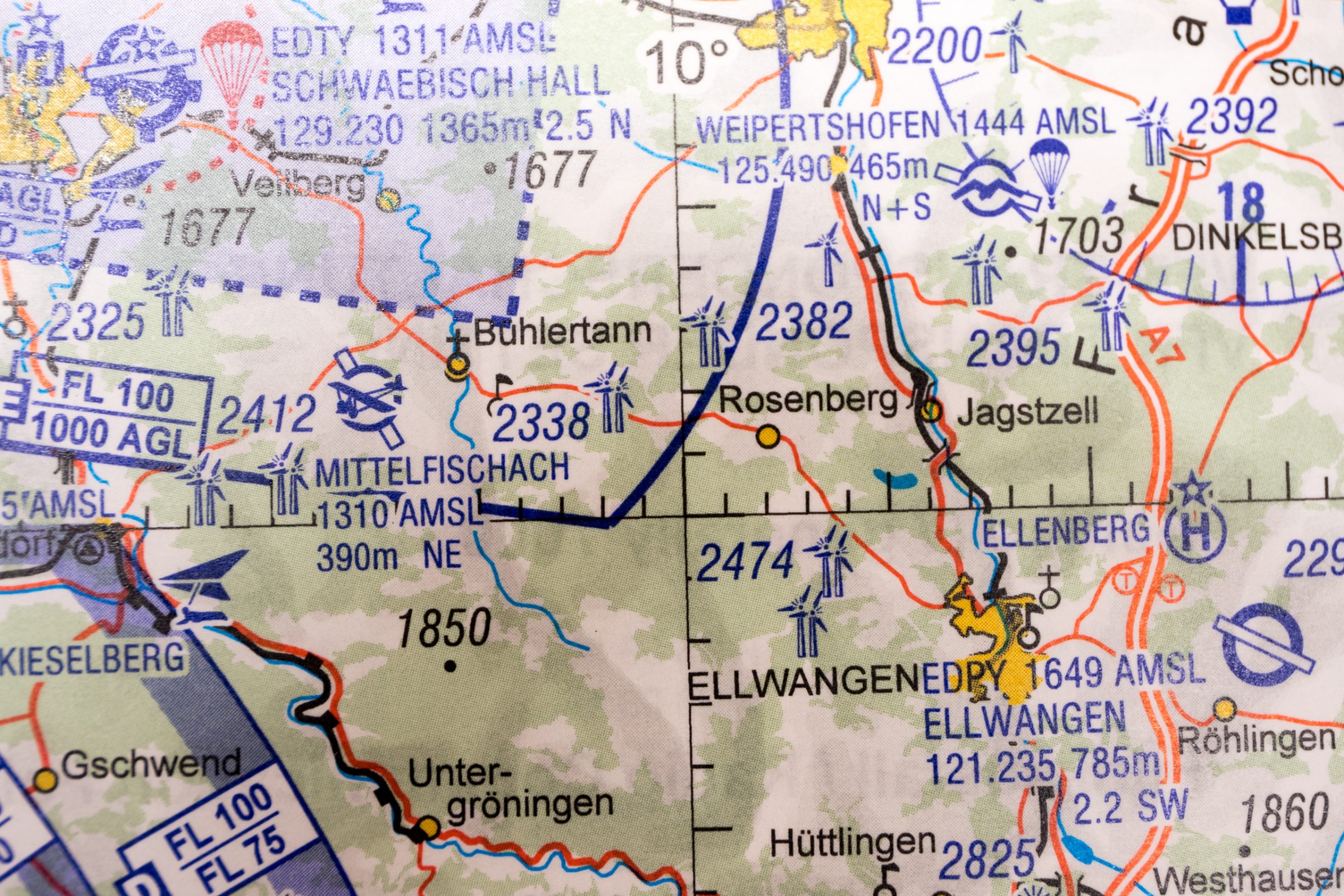
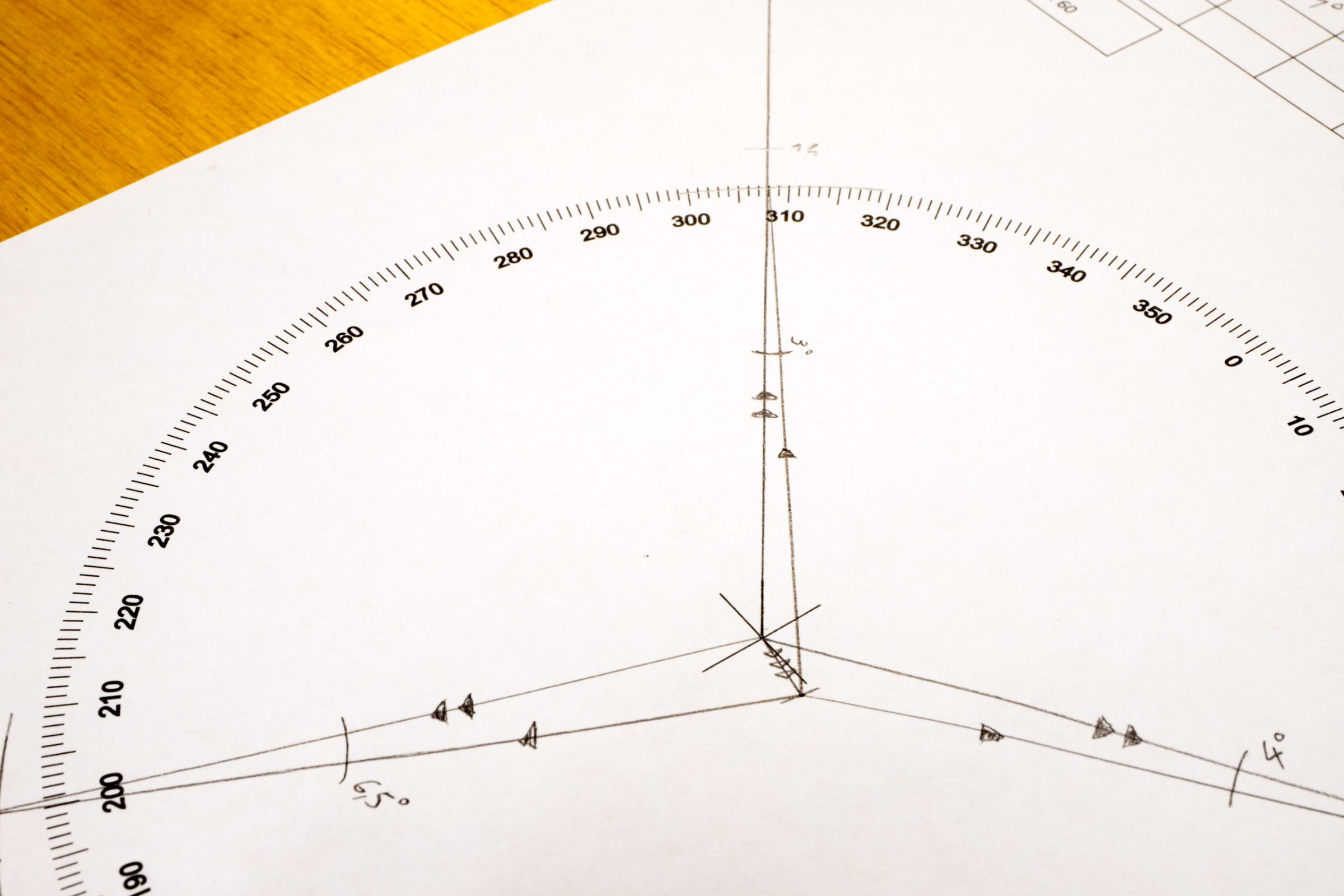
Wichtig ist, dass die vertikal verlaufenden Meridianlinien als Ausgangspunkt für den Winkel zur Kurslinie genutzt werden. Die Kompasrose richten wir an der am nächsten liegenden vertikalen Meridianlinie aus und verschieben sie parallel auf dem Lineal bis wir die Mitte des Flugplatzes treffen. Ihr müsst sicher ein paar Mal nachjustieren, bis ihr die Mitte des Flugplatzes trefft. Wir lesen im nächsten Bild 308° am Winkelmesser ab.
Das gleiche kann auch mit einem Geometriedreieck gemacht werden. Erst das Dreieck an dem Längengrad anlegen und dann parallel mit einem Lineal auf den Startpunkt verschieben. Der Kurs ergibt sich aus dem Basiswinkel 270° + 38° (vom Geometriedreieck abgelesen) = 308°
Der True Course (TC) muss für jeden Streckenabschnitt aus der ICAO Karte einzeln herausgemessen werden.
| von | nach | Entf. | TC | |
| 1 | EDMI | EDPJ | 47 km | 308° |
| 2 | EDPJ | EDNO | 76,5 km | 56,5° |
| 3 | EDNO | EDMI | 76,5 km | 201° |
True Course (TC) Zeichnen
Der True Course (TC) wird in die Windrose des DULV Navigationsblattes eingezeichnet. Man zeichnet den Kurs vom Nullpunkt in der Mitte am Besten gleich bis zum Rand des Blattes. Den jeweiligen Kurs auch gleich mit der Nummer des Streckenabschnittes am äußeren Ende der Linie versehen (1,2,3). Das hilft uns nachher nicht durcheinander zu kommen.
Außerdem versehen wir nun alle unsere drei Kurslinien mit zwei nach außen zeigenden Pfeilen. Diese Pfeile zeigen uns, dass es sich dabei um den True Course (TC) handelt. Auf dem Formblatt seht ihr oben in der Mitte dazu eine Legende.
Die 1h-Linie zeichnen
Mit der 1h-Linie tragen wir in der Navigationsaufgabe eine Distanz ein, die beschreibt wie weit das Flugzeug innerhalb einer Stunde laut True Airspeed (TAS) zurücklegt.
Die True Airspeed (TAS) ist die Geschwindigkeit, die das Flugzeug in Relation zu der umgebenen Luft zurücklegt. Nicht zu verwechseln mit der die Geschwindigkeit, die das Flugzeug gegenüber dem Grund (Ground Speed / GS) zurücklegt. Im Flug sehen wir an der Geschwindigkeitsanzeige nur die True Airspeed. Wenn Ihr z.B. laut Geschwindigkeitsanzeige 200km/h schnell fliegt aber in Wirklichkeit wegen einer Gegenwindkomponente von 50km/h nur 150km/h gegenüber dem Grund zurücklegt ist das ein unglaublich gefährlicher Faktor weil sich damit die Flugzeit auf einmal um 1/4 verlängert und Ihr damit gerade bei längeren Distanzen sehr schnell Spritprobleme bekommen könnt.
Wir wollen die gegebenen 160km/h aus der Vorgabe in das Formblatt übertragen. Jetzt kommt ein kleiner Fallstrick. Eigentlich würde man den Zirkel auf 160mm (16cm) stellen und die Markierung auf den drei Kurslinien vornehmen. Aber unser Formblatt ist nicht groß genug um 16cm vom Nullpunkt aus zeichnen zu können.
Wir müssen jetzt in einem sinnvollen Verhältnis alle Längen verkleinern. Bei 160km/h bieten sich jetzt entweder 1:2 oder 1:3 als Verhältnis an. Wählt das Verhältnis nicht zu groß. Wir werden in einem späteren Schritt auch den Wind mit einzeichnen. Wenn die Streckenlängen wegen einem zu großen Faktor stark schrumpfen haben wir dann ein Problem.
Ich wähle hier 1:2 als Verhältnis. Schreibt das Verhältnis gut sichtbar mit auf das Formblatt. Ab jetzt werden wir alle Längen entsprechend verkürzen oder beim Ablesen verlängern.

Nun den Zirkel in den Nullpunkt einstechen und an jeder von unseren drei Kurslinie leicht abschlagen. Im Anschluss den Schnittpunkt mit „1h“ versehen. Das hilft uns nachher die 1h-Linie von einer weiteren Linie zu unterscheiden, die in den nächsten Schritten dazu kommt.
Tipp: Bei der kompletten Navigationsaufgabe stellen wir den Zirkel nur auf einen einzigen Wert ein. Wir verändern die Spreizung des Zirkels nicht mehr bis zum Ende der Aufgabe. Legt den Zirkel einfach unverändert bis später zur Seite.
Wind umrechnen
Die Windrichtung und -stärke kommt in der Realität von der Wetterberatung bzw. aus dem Selfbriefing und wird in Knoten (9kt in unserem Fall) angegeben. Wir rechnen nun die Knoten in Stundenkilometer um (1kt = 1,852km/h)
9kt = 16,668km/h
Wind Zeichnen
Wichtig: Wind kommt immer AUS einer Richutung. In unserem Fall kommt er AUS 280° und befördert uns in die entgegengesetzte Richtung (360° – 280° = 100°)
Wir zeichnen die Windlinie VON 280° IN Richtung 100°
Wir erinnern uns an den Faktor 1:2 für den wir uns vorhin entschieden haben. Aus „16,668mm“ werden nun „8,334mm“ auf dem Formblatt jetzt 8,334mm in 80° Richtung einzeichnen und am Ende der Linie mit einem Abschlag versehen. Das definiert das Ende der Linie.
Die Windlinie wird mit drei Pfeilen versehen. (Toller Typ, der irgendwann mal definiert hat, dass die kürzeste aller Linien die meisten Pfeile bekommen soll ಠ_ಠ)
Winddreieck zeichnen
Jetzt stechen wir mit dem Zirkel (wir haben ihn nicht verändert!) an das Ende der Windlinie ein und schlagen wieder an jeder Kurslinie einmal ab. Diesmal zeichnen wir den Abschlag deutlich länger als die 1h Markierung, dass wir eine deutliche Unterscheidung dazu haben.
Was sehen wir nun? Der Wind sorgt in dem Beispiel im Bild unten dafür, dass unser zweiter Strich jetzt vor der 1h-Linie liegt. Der Wind, der von der Seite kommt verlangsamt unser Flugzeug etwas. Zum Ground Speed kommen wir aber nachher noch.

Nun verbinden wir das Ende der Windlinie mit unseren neu abgeschlagenen Linien auf der Kurslinie. Diese neuen Linien heißen True Heading (TH) wir versehen sie mit einem Pfeil.
Luvwinkel ablesen
Der Wind treibt unser Flugzeug im Flug in eine bestimmte Richtung. Wenn wir stupide nur unserem Kompass folgen werden wir evtl. unser Ziel verfehlen. Uns interessiert um wie viel Grad Vorhaltewinkel wir fliegen müssen um die Windkomponente auszugleichen.
Jetzt messen wir den Winkel zwischen dem True Course und der neu gezeichneten True Heading.
Entweder lesen wir den Winkel mit dem Winkelmesser ab oder wir legen das Geometriedreieck mit dem Nullpunkt an der Spitze des Dreiecks und verlängern uns die Linie bis zum Ende des Geometriedreiecks.
Wir zeichnen den gemessenen Winkel gleich zu jedem der drei Kurslinien dazu.
| von | nach | Entf. | TC | WCA | |
| 1 | EDMI | EDPJ | 47 km | 308° | 3° |
| 2 | EDPJ | EDNO | 76,5 km | 56,5° | 4° |
| 3 | EDNO | EDMI | 76,5 km | 201° | 6,5° |
Luvwinkel abziehen oder addieren?
Der Wind würde uns aktuell von unserem Kurs abbringen, wenn wir nur dem True Course (TC) folgen würden. Das heißt, wir müssen unseren True Course um den Luvwinkel korrigieren. Nur ziehen wir ihn ab oder addieren wir Ihn?
Kommt der Wind in Kursrichtung von links, müssen wir den Kurs um den Luvwinkel reduzieren (-). Der Luvwinkel wird vom Kurs subtrahiert (-)
Kommt der Wind in Kursrichtung von rechts, müssen wir den Kurs um den Luvwinkel vergrößern (+). Der Luvwinkel wird zum Kurs addiert (+).
Wir legen die Kurslinie von uns weg und schauen woher der Wind kommt. IN diese Richtung korrigieren wir unseren Luvwinkel. In dem unterstehenden Fall kommt der Wind von links, deshalb korrigieren wir unseren Kurs auch nach links – in Richtung eines kleineren Kurses. (-3°)
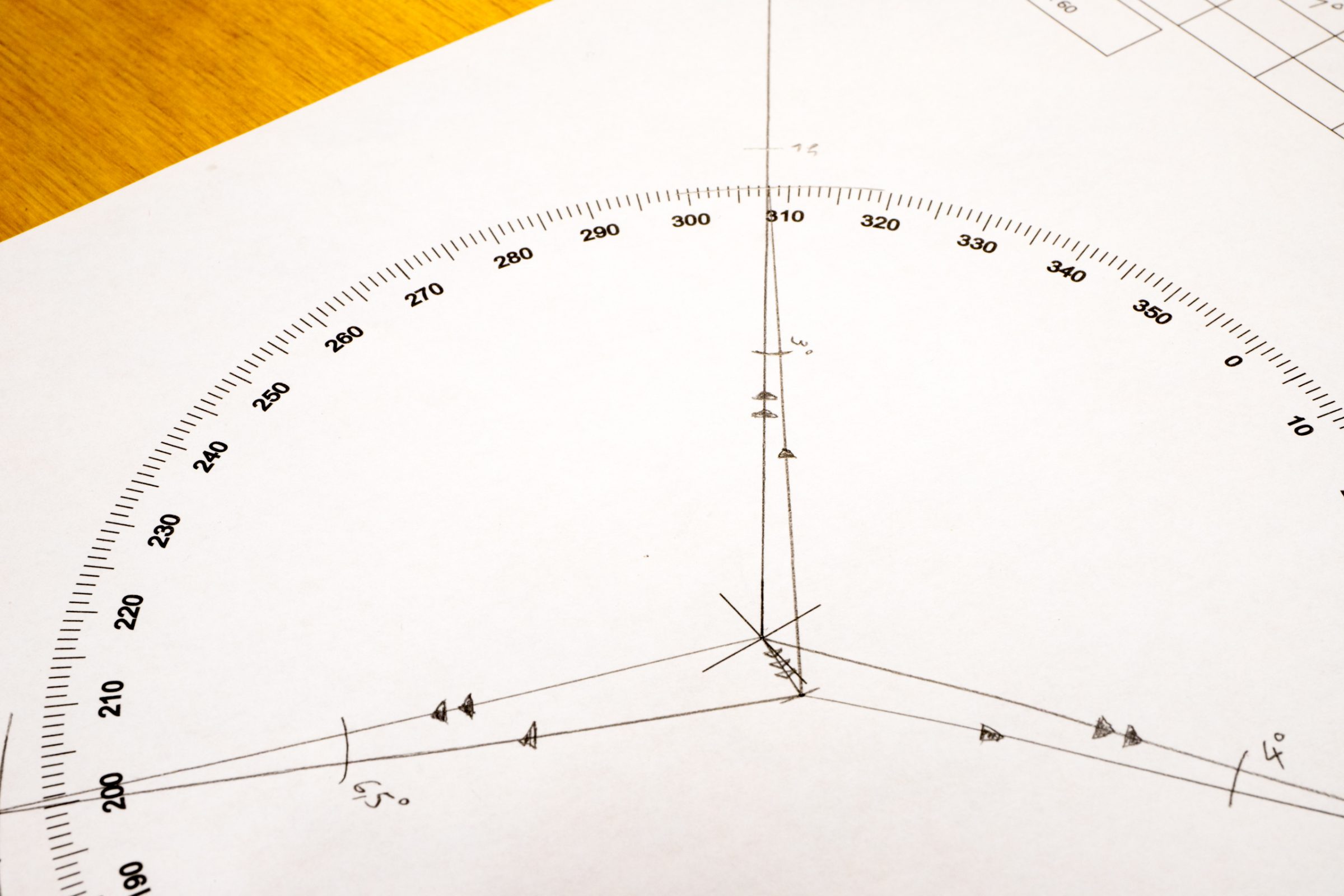
| von | nach | Entf. | TC | WCA | |
| 1 | EDMI | EDPJ | 47 km | 308° | (-3°) |
| 2 | EDPJ | EDNO | 76,5 km | 56,5° | (-4°) |
| 3 | EDNO | EDMI | 76,5 km | 201° | (+6,5°) |
True Heading (TH) ausrechnen
Das True Heading (TH) ergibt sich aus der Summe von True Course (TC) und dem Wind Correction Angle (WCA)
Bsp von EDMI nach EDPJ: 308° -3 ° = 305°
| von | nach | Entf. | TC | WCA | TH | |
| 1 | EDMI | EDPJ | 47 km | 308° | (-3°) | 305° |
| 2 | EDPJ | EDNO | 76,5 km | 56,5° | (-4°) | 51,5° |
| 3 | EDNO | EDMI | 76,5 km | 201° | (+6,5°) | 207,5° |
Die Variation
Es gibt nur wenige Orte auf der Erde wo der geographische Norden gleich dem magnetische Norden ist. Wir müssen eine Korrektur vornehmen, die die Differenz zwischen dem geographischen Norden (dem Norden der ICAO Karte) und dem magnetischen Norden (den der Kompass anzeigt) ausgleicht. Das Erdmagnetfeld verändert sich permanent. Deshalb könnt Ihr auf älteren ICAO Karten eine andere Variation sehen. Außerdem ist es nicht unüblich, dass die Landebahn an einem Flugplatz neue Bezeichnungen bekommen. Die Bezeichnung der Landebahnausrichtung orientiert sich an der magnetischen Nordrichtung.

Auf den ICAO Karten finden sich am oberen Rand eine schwarze, dicke gestrichelte Linie an deren Ende die Variation verzeichnet ist. Diese Linie ist die Isogone. Wie man sehen kann verläuft die Linie der gleichen Variation / Ortsmissweisung nicht parallel mit den Längengraden. In Gebieten wo viel Eisen in der Erde ist kann die Isogone auch in kurven verlaufen. In unserem Fall haben wir eine Variation von „3°E (3° Ost)“.
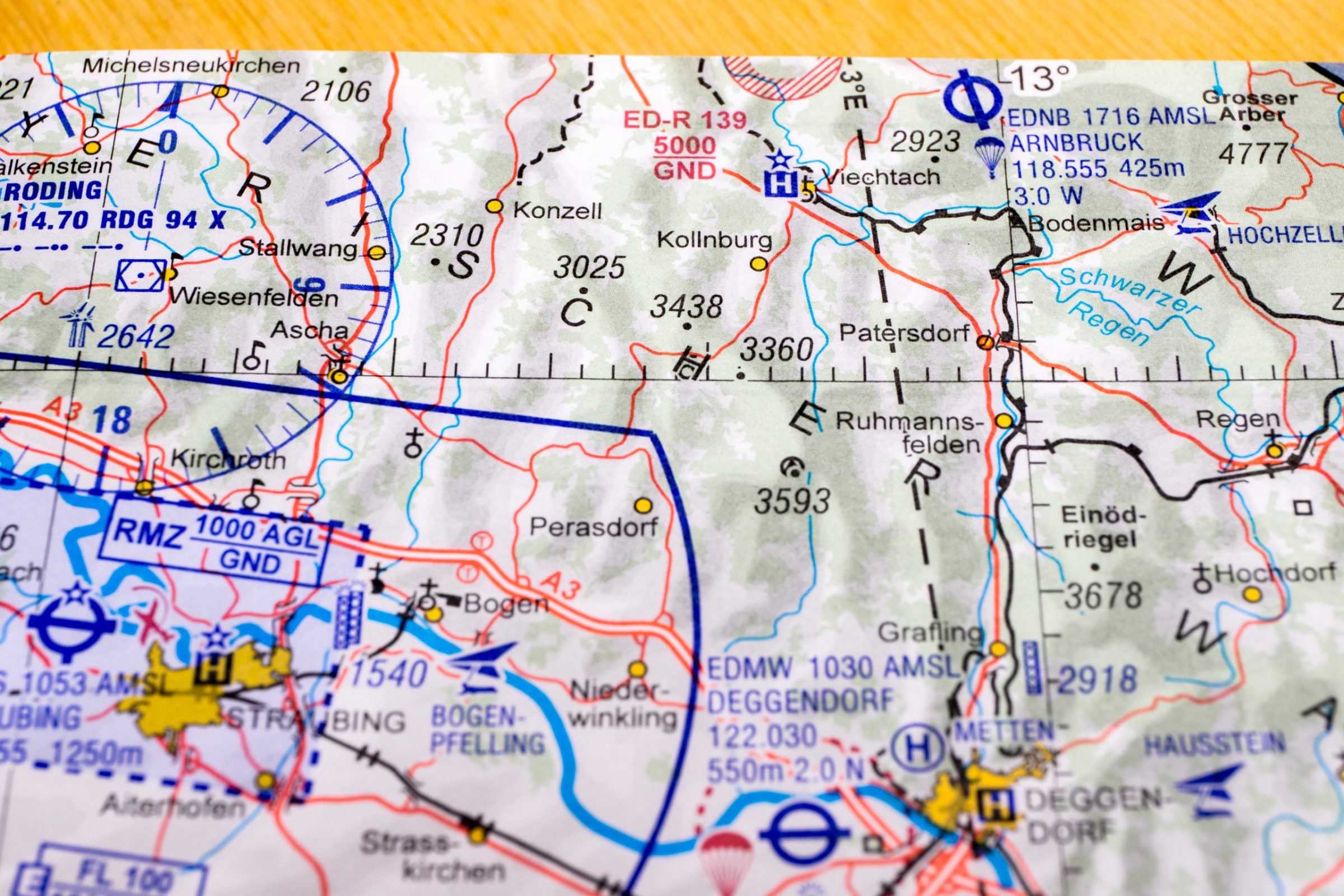
Fliegt man durch Gebiete mit unterschiedlicher Variation muss man die Variation interpolieren oder mehrere Streckenabschnitte rechnen.
Wir wissen nun, dass wir in einem Gebiet mit 3°E Ortsmissweisung fliegen. Die Frage ist nur, addiert man die Variation subtrahiert man diese?
Die Variation muss immer Richtung Norden korrigiert werden.
Fragt Euch: „Was ist nötig um die Variation zu neutralisieren?“
Jedes Grad, das die Variation nach Osten (+) verschiebt müssen wir in Richtung Westen (-) korrigieren und umgekehrt. In unserem Fall befinden wir uns in einem Bereich in dem die Variation 3° Ost beträgt. Wir korrigieren also um 3° nach West.
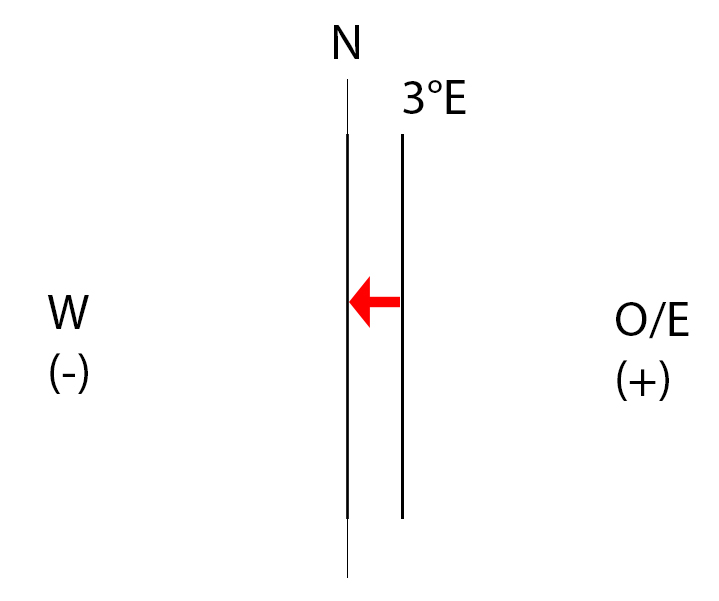
Die Korrektur für unsere Variation beträgt für alle unsere Streckenabschnitte -3°
| von | nach | Entf. | TC | WCA | TH | VAR | |
| 1 | EDMI | EDPJ | 47 km | 308° | (-3°) | 305° | -3° |
| 2 | EDPJ | EDNO | 76,5 km | 56,5° | (-4°) | 51,5° | -3° |
| 3 | EDNO | EDMI | 76,5 km | 201° | (+6,5°) | 207,5° | -3° |
Magnetic Heading (MH) berechnen
Die Magnetic Heading ist die Summe aus dem True Heading (TH) und der Variation (VAR).
305° -3° = 302°
| von | nach | Entf. | TC | WCA | TH | VAR | MH | |
| 1 | EDMI | EDPJ | 47 km | 308° | (-3°) | 305° | -3° | 302° |
| 2 | EDPJ | EDNO | 76,5 km | 56,5° | (-4°) | 51,5° | -3° | 48,5° |
| 3 | EDNO | EDMI | 76,5 km | 201° | (+6,5°) | 207,5° | -3° | 204,5° |
Deviation ablesen
Ist euch mal aufgefallen, dass der Kompass im Cockpit so alleine und weit weg von allen anderen Instrumenten montiert wurde?
Der im Flugzeug verbaute Kompass ist vielen Störquellen ausgesetzt. Metallische Teile aus dem Cockpit, Headsets, Arbeitsströme der Instrumente. Wie kann man also trotz dessen genaue Kurse fliegen? Dazu wird eine sogenannte Deviationstabelle erstellt. Diese gibt für Kursbereichsabschnitte einen Korrekturwert vor. Diese Deviationstabelle ist natürlich Flugzeugindividuell und wird aufwändig vermessen. Die Deviationstabelle sollte an dem Kompass angebracht sein.
Wir orientieren uns nun am Magnetic Heading (MH) und interpolieren die Korrekturwerte aus der Deviationstabelle des Flugzeugs.
Deviationstabellen können in zwei Varianten auftreten:

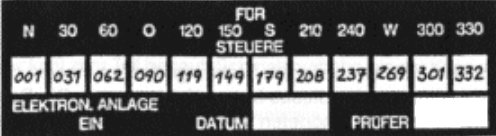
| von | nach | Entf. | TC | WCA | TH | VAR | MH | DEV | |
| 1 | EDMI | EDPJ | 47 km | 308° | (-3°) | 305° | -3° | 302° | +1° |
| 2 | EDPJ | EDNO | 76,5 km | 56,5° | (-4°) | 51,5° | -3° | 48,5° | +1,5° |
| 3 | EDNO | EDMI | 76,5 km | 201° | (+6,5°) | 207,5° | -3° | 204,5° | -1,5° |
Compas Heading (CH) berechnen
Die Compas Heading (CH) ist die Summe aus Magnetic Heading (MH) und der Deviation (DEV)
Bsp EDMI nach EDPJ: 302° + 1° Deviation = 303°
| von | nach | Entf. | TC | WCA | TH | VAR | MH | DEV | CH | |
| 1 | EDMI | EDPJ | 47 km | 308° | (-3°) | 305° | -3° | 302° | +1° | 303° |
| 2 | EDPJ | EDNO | 76,5 km | 56,5° | (-4°) | 51,5° | -3° | 48,5° | +1,5° | 50° |
| 3 | EDNO | EDMI | 76,5 km | 201° | (+6,5°) | 207,5° | -3° | 204,5° | -1,5° | 203° |
Die Compass Heading (CH) ist nun der Kurs den wir für den Streckenabschnitt fliegen, korrigiert um den Wind, die Variation und die Deviation. Mit dem Ergebnis für die Compass Heading (CH) haben wir also unsere ersten Ergebnisse für die Navigationsaufgabe.
Ground Speed (GS)
Je nach Streckenabschnitt haben wir den Wind entweder im Rücken, von Vorne oder von der Seite. Unser Flugzeugs fliegt aber trotzdem in jeder Situation 160km/h laut Instrument. Interessant ist aber wie schnell wir uns gegenüber dem Boden fortbewegen. Diesen Wert können wir aus dem Winddreieck ablesen.
Wir messen die Distanz zwischen dem Nullpunkt unserer Zeichnung und unserem zweiten Zirkelabschlag. Wir messen für Streckenabschnitt 1 72,5mm.
Achtung! Wir arbeiten hier wieder mit Längen. Jetzt müssen wir unseren 1:2 Faktor wieder in Erinnerung bringen. 72,5mm * 2 = 145mm (145km/h). Der Wind, der in dem Fall von vorne links kommt verlangsamt also unsere Geschwindigkeit, die wir über Grund machen um 15km/h.

Die ausgemessenen und umgerechneten Geschwindigkeiten tragen wir als Ground Speed (GS) ein.
| von | nach | Entf. | TC | WCA | TH | VAR | MH | DEV | CH | GS | |
| 1 | EDMI | EDPJ | 47 km | 308° | (-3°) | 305° | -3° | 302° | +1° | 303° | 145 km/h |
| 2 | EDPJ | EDNO | 76,5 km | 56,5° | (-4°) | 51,5° | -3° | 48,5° | +1,5° | 50° | 172 km/h |
| 3 | EDNO | EDMI | 76,5 km | 201° | (+6,5°) | 207,5° | -3° | 204,5° | -1,5° | 203° | 156 km/h |
Flugzeit berechnen
Natürlich wollen wir wissen wie lange wir für den jeweiligen Streckenabschnitt und die komplette Reise benötigen aber viel wichtiger ist die Flugzeit für die Spritberechnung im nächsten Schritt.
Wie lange fliegen wir also für unsere jeweiligen Streckenabschnitte? Wir kennen die Distanz, die wir aus der Karte abgelesen haben (Entf.) sowie die Geschwindigkeit, die wir gegenüber Grund zurücklegen.
Flugzeit = Entf. * 60 / GS
19,45min = 47 km * 60 min / 145 km/h
| von | nach | Entf. | TC | WCA | TH | VAR | MH | DEV | CH | GS | Zeit | |
| 1 | EDMI | EDPJ | 47 km | 308° | (-3°) | 305° | -3° | 302° | +1° | 303° | 145 km/h | 19,45 min |
| 2 | EDPJ | EDNO | 76,5 km | 56,5° | (-4°) | 51,5° | -3° | 48,5° | +1,5° | 50° | 172 km/h | 26,7 min |
| 3 | EDNO | EDMI | 76,5 km | 201° | (+6,5°) | 207,5° | -3° | 204,5° | -1,5° | 203° | 156 km/h | 29,4 min |
| 75,55min |
Die gesamte Flugzeit ergibt sich aus der Summe aller Zeiten für alle Streckenabschnitte. 75,55min
Spritverbrauch berechnen
Nachdem wir wissen wie lange wir für einen Streckenabschnitt unterwegs sind und wir wissen welchen Stundenverbrauch unser Flugzeug hat können wir nun den Verbrauch pro Streckenabschnitt berechnen.
Verbrauch = lt/h * Zeit / 60
5,5l = 17 lt/h * 19,45 min / 60
| von | nach | Entf. | TC | WCA | TH | VAR | MH | DEV | CH | GS | Zeit | Verbrauch | |
| 1 | EDMI | EDPJ | 47 km | 308° | (-3°) | 305° | -3° | 302° | +1° | 303° | 145 km/h | 19,45 min | 5,5l |
| 2 | EDPJ | EDNO | 76,5 km | 56,5° | (-4°) | 51,5° | -3° | 48,5° | +1,5° | 50° | 172 km/h | 26,7 min | 7,57l |
| 3 | EDNO | EDMI | 76,5 km | 201° | (+6,5°) | 207,5° | -3° | 204,5° | -1,5° | 203° | 156 km/h | 29,4 min | 8,33l |
| 75,55min | 21,4l |
Die Summe aller Streckenverbräuche ist nun die Menge an Sprit, die wir für unseren Kurs benötigen werden.
Die Navigationsberechnung, die wir gerade gemacht haben ist die Grundlage für die weitere Flugplanung.
Die Navigation ist nicht nur für die theoretische Prüfung wichtig. Sie bestimmt am Ende in der Realität darüber ob Ihr zum Ziel kommt und dabei nicht unterwegs wegen Gegenwind und Spritmangel in eine Notsituation kommt. Wenn die Berechnung für die Ground Speed nicht passt verfranzt ihr euch bei der terrestrischen Navigation weil die errechneten Zeiten der Legs in der Realität nicht hin kommen werden. Ihr werdet beim Fliegen regelmäßig mit Stift und Papier daheim oder am Flugplatz sitzen und eine Flugvorbereitung machen müssen. Sucht euch zum üben einen Partner der die gleiche Aufgabe parallel rechnet und vergleicht nach jedem Schritt die Ergebnisse und diskutiert diese bei Unstimmigkeiten. Arbeitet exakt und rundet nicht am Anfang schon großzügig auf oder ab. Ihr seht ja, wie viele Schritte notwendig sind bis am Ende so etwas einfaches wie ein Spritverbrauch heraus kommt.
















[…] eine Navigationsaufgabe im Detail abläuft habe ich hier bereits beschrieben. Für die Navigationsplanung sind die Windrichtung und die Windgeschwindigkeit […]
[…] Berechnung machen zu können. Wie eine Navigationsaufgabe auf so einem Blatt ausschaut habe ich hier […]
Hallo, die Berechnung ist gut erklärt.
Nur prüfe mal Deine Berechnung der Windrichtung.
Der Wind kommt aus 280° in Richtung 100° und nicht in Richtung 80°
Grüße Mathias
Oh, danke für den Hinweis. Ich habe es im Text korrigiert. Blöd, richtig gezeichnet war es ja.
Danke dir. Ich sitze gerade an der Vorbereitung zur theoretischen Prüfung und so richtig haben wir das im Kurs gar nicht durchgenommen. Ich komme jetzt langsam immer selbstständiger voran.
Erstmal vielen Dank für die Ausführliche Beschreibung und Erklärung.
Mir macht die Deviation immer noch Kopfschmerzen:
Nehmen wir das Beispiel der abgebildeten Deviationstabellen.
In der oberen steht bei einem Kurs von 300 eine Deviation von -1.
In der unteren bei einem Soll von 300 ein „steuere“ 301.
Anders ausgedrückt: ich muss laut Kompass 301° fliegen um einen Kurs von 300° zu halten. Oder wenn ich laut Kompass 300° fliege, fliege ich in Wahrheit 299°.
Ist die Deviation dann nicht wie in der Tabelle auch angegeben -1?
In der Berechnung wird allerdings dann die Deviation als +1° angegeben.
Das Ergebnis ist am Ende richtig, aber müsste ich von meinem MH nicht die Deviation abziehen? Sprich in dem aufgeführten Beispiel von EDMI nach EDPJ mit einem MH von 302°
302° – (-1°) = 303°
Und von EDNO nach EDMI mit einem MH von 204,5°
204,5° – (+1,5°) = 203°
richtig sein?
Wenn nicht, wie Löse ich den Knoten in meinem Kopf, dass die obere Deviationstabelle bei 300° eine Deviation von -1 ausweist aber das im Grunde dann +1 ist?
Danke schon mal im Voraus 🙂
Grüße
Kosta